Les statistiques sont un outil ultra puissant pour un data scientist. D’une manière générale, les statistiques consistent à utiliser les mathématiques pour effectuer une analyse technique des données. Une visualisation de base telle qu’un diagramme en camembert peut vous donner des informations de haut niveau, mais avec des statistiques, il est possible d’exploiter les données de manière beaucoup plus ciblée et davantage basée sur les informations. Les statistiques aident à proposer des conclusions concrètes sur nos données.
En utilisant des statistiques, on peut obtenir des informations plus détaillées sur la structure exacte de nos données et sur la manière dont nous pouvons appliquer de manière optimale d’autres techniques de science des données pour obtenir davantage d’informations. Dans cet article, nous allons examiner 5 concepts statistiques qu’il faut connaître et comment ils peuvent être appliqués le plus efficacement possible.
Les Caractéristiques Statistiques
Les caractéristiques statistiques sont le concept statistique le plus utilisé en data science. C’est souvent la première technique de statistiques que vous appliquez lors de l’exploration de vos données. Dans ces caractéristiques on retrouve la variance, la moyenne, la médiane, les centiles et bien d’autres.
Un box plot illustre parfaitement ce que nous pouvons faire avec des fonctionnalités statistiques de base:

Lorsque la boîte à moustaches est courte, cela signifie que la plupart de vos points de données sont similaires, car il existe de nombreuses valeurs dans une petite plage.
Quand le diagramme en boîtes est haut, cela signifie qu’une grande partie de vos points de données est très différente. Car les valeurs sont réparties sur une large plage.
Si la valeur médiane est plus proche du bas, nous savons que la plupart des données ont des valeurs inférieures. En revanche, si la valeur médiane est plus proche du sommet, nous savons que la plupart des données ont des valeurs plus élevées. Si la ligne médiane ne se trouve pas au milieu de la boîte, il s’agit d’une indication de données asymétriques.
Les moustaches sont-elles très longues? Cela signifie que vos données ont un écart-type et une variance élevés. C’est-à-dire que les valeurs sont très variables. Si vous avez de longues moustaches d’un côté de la boîte mais pas de l’autre, vos données peuvent varier fortement dans une seule direction.
Distributions de probabilité
La probabilité est le pourcentage de chance qu’un événement se réalise. En Data science, ceci est généralement quantifié dans la plage de 0 à 1. Le 0 signifiant l’événement ne se produira pas et 1 signifiant que cela se produira. Une distribution de probabilité est une fonction qui représente les probabilités de toutes les valeurs possibles dans l’expérience.
Les plus connues:

La distribution uniforme.
- Il s’agit bien d’une distribution «tout ou rien». On peut aussi y voir une indication d’une variable catégorielle à 2 catégories: 0 ou la valeur. Votre variable catégorielle peut avoir plusieurs valeurs autres que 0, mais nous pouvons toujours la visualiser de la même manière, comme une fonction par morceaux de plusieurs distributions uniformes. Tous les intervalles de même longueur inclus dans le support de la loi ont la même probabilité. Cela se traduit par le fait que la densité de probabilités de ces lois est constante sur leur support.

La distribution normale
- Communément appelée distribution gaussienne, est spécifiquement définie par sa moyenne et son écart type. La valeur moyenne modifie la distribution dans l’espace et l’écart-type contrôle la propagation. Ainsi, avec une distribution gaussienne, nous connaissons la valeur moyenne de notre ensemble de données ainsi que l’étendue des données, c’est-à-dire qu’elles sont réparties sur une large plage ou très concentrées autour de quelques valeurs.
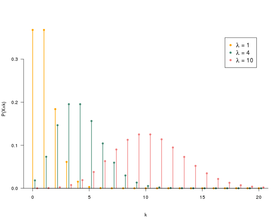
Une distribution de Poisson
- Elle est similaire à la normale mais avec un facteur d’asymétrie ajouté. Avec une faible valeur d’asymétrie, une distribution de poisson aura une répartition relativement uniforme dans toutes les directions, tout comme la normale. Mais lorsque la valeur d’asymétrie est élevée, la diffusion de nos données sera différente dans des directions différentes; dans un sens, il sera très répandu et dans l’autre, il sera très concentré.
Il existe de nombreuses autres distributions dans lesquelles vous pouvez vous plonger, mais celles-ci nous donnent déjà beaucoup de valeur. Nous pouvons rapidement voir et interpréter nos variables catégorielles avec une distribution uniforme. Si nous voyons une distribution gaussienne, nous savons qu’il existe de nombreux algorithmes qui fonctionneront bien par défaut avec la gaussienne, nous devrions donc les choisir. Et avec Poisson, nous verrons que nous devons faire très attention et choisir un algorithme robuste aux variations de la dispersion spatiale.
Réduction de la dimension
En statistique, apprentissage automatique et théorie de l’information, la réduction de dimensionnalité ou réduction de dimension est le processus de réduction du nombre de variables aléatoires considérées en obtenant un ensemble de variables principales. Il peut être divisé en sélection et extraction de caractéristiques. Le terme réduction de dimension est assez intuitif à comprendre. Nous avons un jeu de données et nous aimerions réduire le nombre de dimensions dont il dispose. En science des données, il s’agit du nombre de variables de caractéristiques.
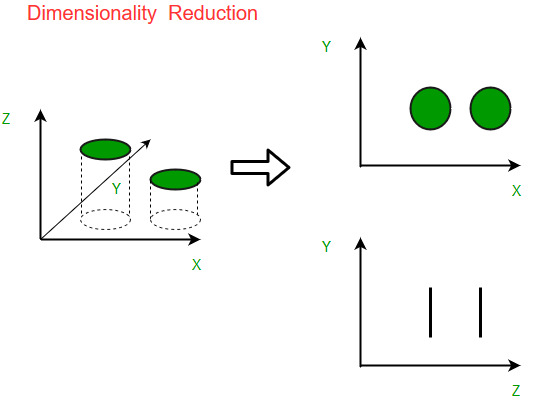
La technique de statistiques la plus populaire qui est utilisée pour la réduction de la dimension est le PCA, qui crée des représentations vectorielles de caractéristiques montrant leur importance pour leur corrélation. PCA peut être utilisé pour appliquer les deux styles de réduction de dimensionnalité décrits ci-dessus.